Types as relations

While doodling programs with types on paper, I found something interesting that I want to share with you.

Symbolic relations

Let’s start by defining the natural number.

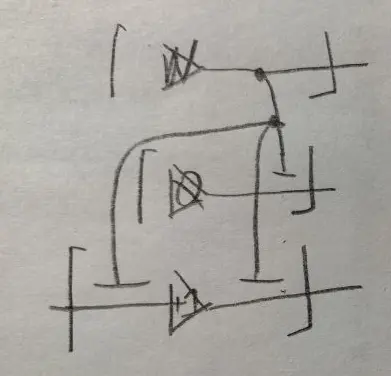
$Nat$ _
$Zero$ _
_ $Succ$ _

Zero x := [
    $Zero$ x
    $Nat$ nat
    nat $Type x
]
x Succ y := [
    x $Succ$ y
    $Nat$ nat
    nat $Type x
    nat $Type y
]

Here, $Nat$, $Zero$, $Succ$ are one-to-one relations. It is the kind of relation you will find in relational databases.

However, what is the type of $Nat$?

“Type of”

In Idris 2, Nat : Type and Type : Type.

In Lean 4, Nat : Type 0 and Type 0 : Type 1.

In our case, we don’t have a type system, only relations. $Type is a one-to-many relation.

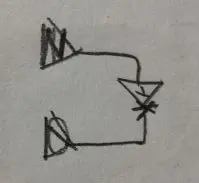
Relation names are used during unification, and there isn’t anything special about $Type. You can use any amount of relations.

Unification, cut, alternation

Instead of elimination, we have cut and alternation (backtracking). We do lose the ability to have match exhaustively, and a program may fail while reducing. On the up side, pattern matching and type checking are now the same.

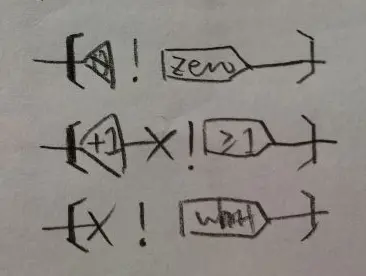
x Example y := [
    Zero x
    !
    "zero" = y
] | [
    _ Succ x
    !
    ">=1" = y
] | [
    "what" = y
]

The unification rule for one-to-one relation is as follows:

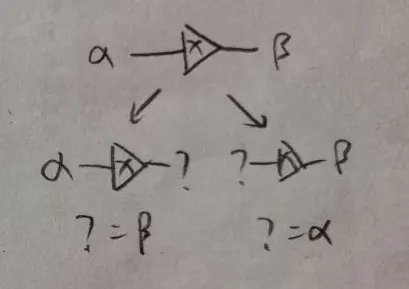
For one-to-many, only one of the branch is true.

If you have used unique constraints in SQL, this should make sense to you.

Full fnification rules

I have listed all the rules of unification in this system, borrowing the syntax from interaction nets. All rules are reversible.

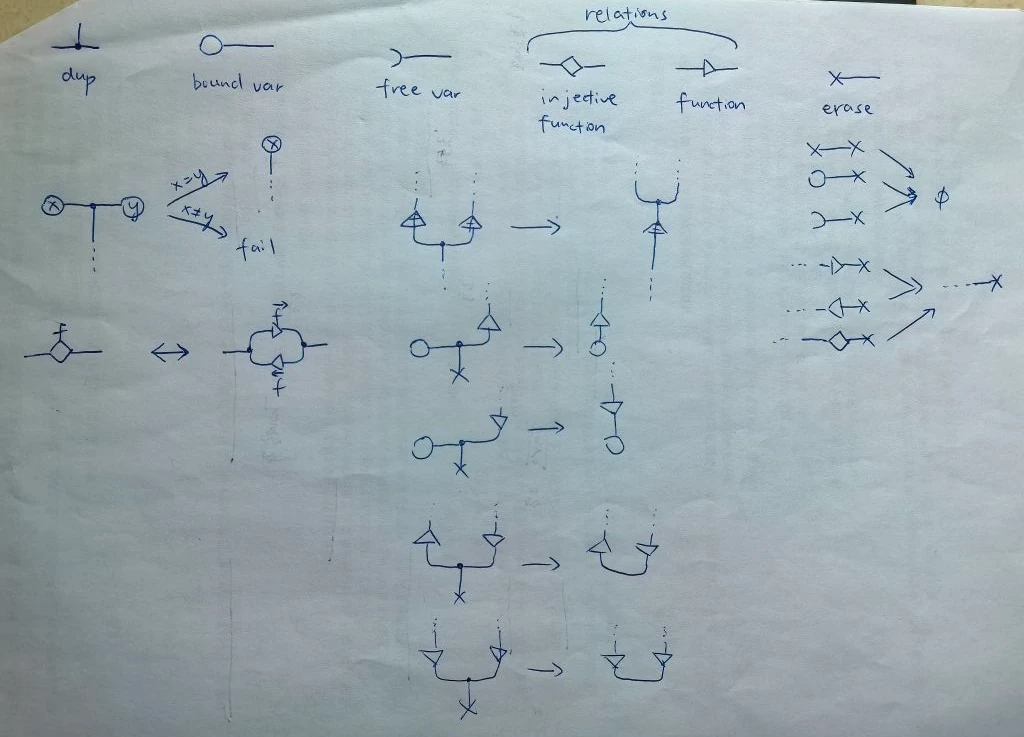
You can clearly see the similarity to lambda calculus, interaction nets, minikanren and concatenative calculus.

A compiler for this language does not need to implement value numbering or constant folding. It is done by the language itself.

Conclusion

It seems that you don’t need a type system to make your program annotated and safe. The relational logic system I found here is different from both Prolog and minikanren. In addition, I have never seen a relational database with free variables.

The next logical step would be to implement a language/database based on this system.

Additional words

A similar idea can be found inside the Pure programming language.

I/O effects should be implicit cut, while pure computation can be backtracked easily.