Nested Taiji Holes

Acknowledgement

The idea of nested holes was originally discovered as part of algograph, although the author still called it “effects” back then.

A discussion in the vague direction of LISP with screwlisp has prompted me to clarify the idea of nested holes.

The idea of monad comes from Idris 2.

The idea of algebraic effect comes from Koka.

Introduction

A program can only run when it fully exists. If a part of it exists not, the computation happens not. What does “exist” mean though?

This article talks about the shape of algorithms (“type”), not the implementation of them (“term”).

We shall call a hole “positive” if it “exists”; “negative” otherwise.

This idea is outside what can be described by total functions in Constructions Calculus.

Nested holes in practice

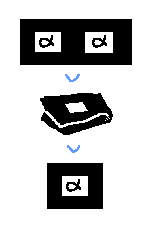
An ELF file is a positive hole with many negative holes with positive holes inside them. The interpreter (linker) provided by the operating system links the program together before running. The kernel fills the rest of the holes by itself.

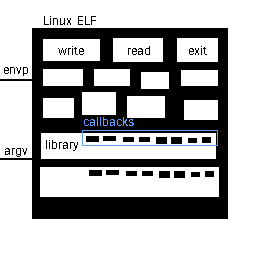
Syscalls are holes to be filled in by the kernel. Dynamic libraries used are holes that may or may not contain syscall holes or other dynamic library holes.

Nested holes in theory

Child holes of a hole are not ordered. They are a unordered set.

Mathematics seem to not care which color of hole exists, Yin or Yang. Yin may swap place with Yang. We only observe the two distinct colors.

A thought: Generative algorithms may fill a hole automatically, or there are other ways to make a negative hole directly compute.

Hole type matching

At the type system level, it is possible to introduce a hole. The final algorithm may ignore whatever passed in from the created hole.

At the type system level, it is not possible to remove a hole without filling it in. Still, if one knows the implementation of the hole outside, they can rewrite it to remove the hole.

A hole is either inside or it doesn’t exist, although this “exist” means differently than the negative hole which “doesn’t exist” but still exists.

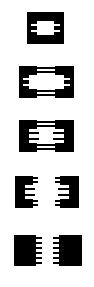
Recursive holes

Recursion is possible. If you accept the fact that algorithm blocks compose naturally like this, the combinators in To Mock a Mockingbird become typed.

For the type on the left (in the image below), it is possible to plug it with itself, or have a few of those blocks chain together into a ring.

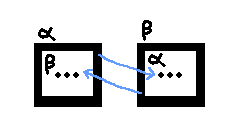
Two mutually recursive holes fit into one another.

In C, program linking is usually done by the following two steps.

1. At compile time, Part A is linked together with Part B by the ld linker.
2. At run time, Part A calls B::init(A::func) to link itself properly with Part B.

Mathematically, there is no difference between compile time linking and run time linking. Even time itself is relative.

Folding holes

If you have two holes of the same shape, they can be folded into one hole.

In the eyes of the compiler for a language using this theory, it is simpler to handle than algebraic effects.

Improvement over entangled algebraic effects

You may ignore this section if you don’t know algograph already.

To put it simply, the idea that algebraic effects might entangle with each other is that, [a program with the ability to product effect A and effect B] has a different type from [a program with the ability to product effect A and effect B but not both at the same time]. This gets complicated fast, as more effects are added to a block of code, the combination explodes. Text-based algorithmic languages like Koka choose to not observe this fact and make every effect exclusive of CPU time. The loss of information (different ways of how effects may entangle) leads to fewer optimization opportunities by a compiler that has any sense of locality (not a “full program compiler”).

Real world type checker support

Zig: No.

fn foo(foo1: @TypeOf(foo), bar: i32) i32 {
    if (bar > 0) {
        return foo1(bar - 4);
    }
    return bar;
}

fn a(comptime B: type) fn (B, i32) i32 {
    return opaque {
        fn f(b1: B, x: i32) i32 {
            if (x % 2 == 0) return b1(x / 2);
            return b1(x * 3 - 1);
        }
    }.f;
}

fn b(comptime A: type) fn (A, i32) i32 {
    return opaque {
        fn f(a1: A, x: i32) i32 {
            if (x % 3 == 0) return a1(x / 3);
            return a1(x * 5 - 1);
        }
    }.f;
}

const a_applied = a(@TypeOf(b(@TypeOf(a_applied))));

test {
    _ = foo;
    _ = a_applied;
}

$ zig test taiji-holes.zig
taiji-holes.zig:1:1: error: dependency loop detected
fn foo(foo1: @TypeOf(foo), bar: i32) i32 {
^~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
referenced by:
    test_0: taiji-holes.zig:29:9

C++: No.

#include <functional>

using FooFunc = std::function<int(FooFunc, int)>;
                               // ^ FooFunc is not defined

Lean: Sort of.

A friend has pointed out that Lean has the refine tactic that deals with holes.

At type level: don’t know.

Function “coloring”

What is the “coloring” in “function coloring”? Note that the “coloring” here means totally different from the Taiji coloring above.

What is async fn(A) -> B?

Is it monad? A -> Future B

Is it effects? A -> <async> B

Analogous to how holes form in bread and cheese, let us call the different nesting of holes different “foamings”.

The function coloring simply comes from the fact that the language cannot treat types as regular values, plus it does not support native foaming.

Looking at async/await in Zig, the “async” effect has holes that implicitly receive a type as input:

xasync: fn (func, args, stack) Frame(ReturnType(@TypeOf(func)))

Therefore, we shall say that function coloring is an artifact of dependent types and foaming.

More colors, more symmetry groups

Why only two-fold symmetry $C_2$? If planar portals can be nested in a variety of ways, maybe algorithms can employ any symmetry group?

Placed here as a thought exercise.

Culture relevance

A discourse of 玄 in the book《太玄》discuss about the development of real life events under a ternary system. It is safe to say that I do not yet understand any of that book.